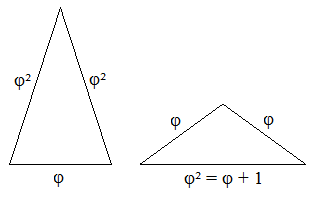Sciences : Coincidences troublantes et fascinantes

[Sylia]

Bonjour !
J'ai parcouru les différents sujets présents sur le forum, et je pense que le mien est nouveau, alors je tente le coup !

Etant une étudiante en mathématiques, il m'est arrivé au cours de mon cursus d'apprendre certaines propriétés scientifiques qui m'ont laissée complètement scotchée (et le terme est faible).
Par exemple, peut-être avez vous déjà entendu parler des racines n-ièmes de l'unité ? Pour les plus curieux, je laisse une petite définition Wikipédia :

Hors-sujet

En mathématiques, étant donné un nombre entier naturel non nul n, une racine n-ième de l'unité (parfois appelée nombre de de Moivre du nom d'Abraham de Moivre) est un nombre complexe dont la puissance n-ième vaut 1.

. Ce qui est réellement fascinant, c'est que lorsqu'on place ces racines sur un cercle trigonométrique, elles forment un polynôme régulier à n côtés. Rien ne laissait présager ce phénomène, et pourtant il existe bel et bien, peu importe la valeur de n.

Après avoir découvert cette incroyable coincidence, je me suis rendue compte que l'univers entier était fait de ces hasards : je pense bien évidemment aux lois physiques décrites par des formules si simples, alors que notre monde est si complexe. J'ai alors décidé de faire quelques recherches sur le net et suis tombée sur un article qui posait une question assez pertinente : Pourquoi le monde se conforme t-il à des lois numériques et mathématiques ?

Même si les lois scientifiques nous paraissent à tous évidentes et naturelles, on peut se dire que s'il existe des formules qui expliquent le fonctionnement de notre monde, il doit en exister pour comprendre le fonctionnement des rapports sociaux, du "destin", et de tant d'autres choses. Alors les coincidences du quotidien, ne seraient en fait plus des coincidences, mais des phénomènes répondant à des formules spécifiques et récurrentes, comme si le fonctionnement de notre monde était calqué selon un motif prédéfini. Ca me fait penser à une série d'ailleurs : Touch (peut-être certaines connaissent et comprendront le lien).

J'avoue pousser la réflexion un peu loin, pour au départ de simples racines complexes

J'aimerais avoir des avis là-dessus, et si vous avez fait face à un de ces hasards mathématiques troublants, j'apprécierai grandement que vous me scotchiez à nouveau ! Si je n'ai pas été assez cohérente dans mes propos (ce qui ne m'étonnerai guère), je m'en excuse d'avance.

[Mei Citron]

Ce qui est réellement fascinant, c'est que lorsqu'on place ces racines sur un cercle trigonométrique, elles forment un polynôme régulier à n côtés. Rien ne laissait présager ce phénomène, et pourtant il existe bel et bien, peu importe la valeur de n.

Est-ce que tu voulais dire plutôt un polygone régulier à n côtés ?
Les polynômes sont des courbes de fonction sur les axes x et y. Quoique, ça peut effectivement se dire comme ça aussi, visuellement ça rend la même chose.
Je n'avais pas du tout pensé à transposer la racine de l'unité sur un cercle trigonométrique et effectivement ça surprend de voir apparaître un polygone (ou polynôme polygonal) si on aborde la chose d'un regard néophyte, regard qu'est le mien. J'imagine que les matheux baignés dedans depuis des années trouveraient ça tellement banal. xD

Je ne saurais absolument pas expliquer ce genre de phénomènes mais je pense que la plupart des scientifiques/mathématiciens philosophes pourraient effleurer la chose. Je pense notamment au Réalisme scientifique et à l'Instrumentalisme. Et puis certain-e-s ici pourraient aussi apporter leur éclairage.
"Pourquoi le monde se conforme t-il à des lois numériques et mathématiques ?"
Serait-ce plutôt : les lois numériques et mathématiques expliqueraient le monde de notre regard d'humain-e ?
Ou : Nous sommes nous inspiré-e-s de la nature pour établir ces lois numériques et mathématiques ?

et si vous avez fait face à un de ces hasards mathématiques troublants, j'apprécierai grandement que vous me scotchiez à nouveau !

Je me suis détachée des maths (dans le sens académique) après mon bac mais j'utilise toujours le nombre d'or pour faire certaines proportions et perspectives dans mes dessins.
Le nombre d'or est égal à , soit environ 1.61803398875 et est défini comme une proportion parfaite, dite aussi "divine proportion", dans la peinture, dans la sculpture, dans l'interprétation de la nature (par la religion judéo-chrétienne) et dans l'architecture. L'objet ou le sujet donne un sentiment d'harmonie et d'équilibre, et parfois de quiétude et de plaisir.

On se réfère souvent à la spirale infinie formée dans l'assemblage d'un rectangle découpé en nombre d'or :

► Afficher le texte

Ce qui est fascinant c'est qu'on retrouve cette spirale partout dans la nature si on regarde bien, par exemple dans certains coquillages, la pomme de pin, la coquille d'escargot, dans certaines fleurs (agencement et taille des pétales), etc.

Je connais surtout son utilisation dans la peinture et la conception des personnages humains. Puis on dit souvent que si le corps d'une femme respecte les proportions du nombre d'or, alors cette femme est physiquement parfaite (je ne fais que rapporter des propos hein...).

On parle aussi de triangle d'or (que j'utilise aussi parfois pour faire certaines perspectives) étant simplement un triangle isocèle dont les côtés sont dans le rapport du nombre d'or :

► Afficher le texte

Dans un tableau assez connu :
La naissance de Vénus, de Sandro Botticelli (1482-1485).

► Afficher le texte

D'autres exemples de productions basées sur le nombre d'or à travers le monde entier :
http://lenombredor.wikispaces.com/Histoire
Je ne peux pas confirmer l'origine de l'expression "nombre d'or" mais ce site-là en propose une :

Le nombre d'or est un terme apparu au début du XXe siècle. C'est aussi durant ce siècle que Théodore Cook introduit, pour désigner le nombre d'or, la lettre grecque phi (φ) en l'honneur du sculpteur grec Phidias qui décora la façade du Parthénon à Athènes notamment avec la statue d'Athéna (où l'on peut retrouver la présence du nombre d'or).
Pour désigner ce nombre, les Grecs n'avaient pas de nom spécifique. Luca Pacioli lui donna pour nom "divine proportion" et Kepler "sectio divina". Dans les deux cas nous retrouvons le mot divin car tous les deux considéraient que le nombre d'or est unique comme Dieu et car ce nombre est régi par trois termes (allusion ici à la Sainte -Trinité). De plus, ce nombre est irrationnel, soit hors de la raison humaine, donc extra-humain. Léonard De Vinci le nommait "sectia aurea".

Si je peux proposer le livre que j'ai lu : Géométrie du Nombre d'Or, de Robert Vincent.

Je trouve le phénomène tout autant fascinant. En fait, je suis toujours fascinée par les mathématiques dans leur ensemble et ce qu'elles produisent de façon tangible et visuelle (les courbes et les "dialectiques" à inconnues) mais ça doit être mon regard de graphiste qui me fait sentir les choses comme ça.

Puis pour se détendre un peu et parce que j'adore :

► Afficher le texte

[A.O.Barnabooth]

Quaternité, blog de Rémi Schulz, pourrait t'intéresser : il s'intéresse aux coïncidences, essentiellement numériques (nombre d'or, suites de Fibonacci, quaternité, etc.).

[Thalweg]

Dans le genre, c'est en rassemblant une série de mises en équations de phénomènes physiques que je me suis rendu compte que beaucoup de phénomènes physiques différents peuvent s'expliquer par les mêmes équations, ce qui en soit m'a paru assez singulier sur le coup.

A mon avis, d'autres avant moi y ont pensé et les petits-enfants de ceux-là sont en train de se tuer à faire émerger une théorie du tout, équation unique simplissime qui pourrait tout expliquer. Ils cherchent toujours, mais ont fait des progrès. D'où univers à 11 dimensions, et la porte à côté.

Exemple de ces phénomènes ? Gravitation (newtonienne, pas avec Einstein) et électricité statique. Les deux lois disent que deux corps sont attirés (ou repoussés) par une force proportionnelle au produit de leurs masses ou de leurs charges et inversement proportionnelle au carré de la distance qui les sépare.

Quant à la question soulevée par Mei, je vais avancer une réponse qui me paraît farfelue, bien que je la trouve ayant une certaine logique : pour qu'il puisse avoir du sens pour les intelligences qui peupleront l'univers ? Autrement tourné, sans ces lois mathématiques gouvernant l'univers, nous n'existerions pas, ergo la question ne se poserait pas non plus. C'est un peu le serpent qui se mord la queue, mais je n'ai pas de meilleure interprétation.

D'après une théorie, le jour où quelqu'un découvrira exactement à quoi sert l'Univers et pourquoi il est là, ledit Univers disparaîtra sur-le-champ pour se voir remplacé par quelque chose de considérablement plus inexplicable et bizarre. Selon une autre théorie, la chose se serait en fait déjà produite.

[Sylia]

J'ai pris le temps d'aller visiter tous les liens que vous m'avez si gentiment offert, et je vous en remercie parce que je les trouve très pertinents.

Est-ce que tu voulais dire plutôt un polygone régulier à n côtés ?

Oui, je m'excuse, c'est évidemment un polygone et non un polynôme ! Je faisais des exercices sur les ensembles de polynômes à ce moment-là, ce qui explique l'erreur

Je me suis détachée des maths (dans le sens académique) après mon bac mais j'utilise toujours le nombre d'or pour faire certaines proportions et perspectives dans mes dessins.

Bien que n'ayant jamais entendu le terme "nombre d'or" auparavant, j'ai eu une forte impression de déjà vu en lisant la formule mathématique de ce nombre. Je suis donc partie fouiner dans mes cours, et je l'ai finalement trouvé : j'ai eu l'occasion d'étudier en profondeur la suite de Fibonacci auparavant, et j'étais en effet tombée sur ce terme-là.
Après ton explication, il prend forcément une dimension tout autre à mes yeux. Je suis également intéressée par les arts puisque je dessine un peu, et faire face à l'apparition de ce nombre dans des oeuvres si connues me déroute. Si tu voulais me scotcher : c'est réussi !
Je pense lire le livre que tu m'as recommandé puisqu'il a l'air fort intéressant

"Pourquoi le monde se conforme t-il à des lois numériques et mathématiques ?"
Serait-ce plutôt : les lois numériques et mathématiques expliqueraient le monde de notre regard d'humain-e ?
Ou : Nous sommes nous inspiré-e-s de la nature pour établir ces lois numériques et mathématiques ?

Cet aspect du problème me semblait aussi possible. Evidemment, l'être humain est à l'origine de ces lois, puisqu'il a lui-même posé des axiomes qui ne peuvent être prouvés, et dont toutes les autres lois découlent. Cependant, ces axiomes sont des propriétés qui sont évidentes même sans démonstration. On ne peut pas prouver que 1+1 = 2 (ce qui d'ailleurs peut être faux en fonction de la base dans laquelle on le calcule...). Alors, les coincidences apparaissant dans les lois déduites n'ont pas pu être anticipées par l'homme. On en revient un peu au problème de "l'oeuf et la poule". On ne peut savoir qui est la cause et qui est la conséquence.

Puis pour se détendre un peu et parce que j'adore

Ces images sont vraiment hilarantes (oui, je fais partie de ces rares personnes que les maths font parfois rire ). J'en ai profité pour les enregistrer, et les partager aux connaisseurs. Au passage, cette cardioïde est réellement sublime

Quaternité, blog de Rémi Schulz, pourrait t'intéresser : il s'intéresse aux coïncidences, essentiellement numériques (nombre d'or, suites de Fibonacci, quaternité, etc.).

Je suis allée y faire un tour, et même si je n'ai encore eu le temps de tout regarder, j'ai trouvé deux/trois éléments très intéressants. Merci beaucoup

Exemple de ces phénomènes ? Gravitation (newtonienne, pas avec Einstein) et électricité statique. Les deux lois disent que deux corps sont attirés (ou repoussés) par une force proportionnelle au produit de leurs masses ou de leurs charges et inversement proportionnelle au carré de la distance qui les sépare.

J'ai beau connaitre ces deux formules depuis la nuit des temps et avoir remarqué la similitude, j'avoue ne m'être jamais arrêtée dessus.

A mon avis, d'autres avant moi y ont pensé et les petits-enfants de ceux-là sont en train de se tuer à faire émerger une théorie du tout, équation unique simplissime qui pourrait tout expliquer. Ils cherchent toujours, mais ont fait des progrès.

Lorsque je tombe sur des similitudes entre des domaines variés, je tends également à penser que cette équation magique existe peut-être. J'ai lu dans ta présentation que tu avais été impressionné par l'existence des orbitales électroniques. Ca a eu le même effet pour moi. Cette simple existence permet d'expliquer les liaisons les plus grandioses de notre univers, mais ce concept m'a fait penser à toute autre chose : les relations humaines. En effet, on observe de même des liaisons entre deux parties permettant de les rendre plus stable ou moins stable. Même si ici, le terme de stabilité n'est plus physique mais psychologique en général. C'est en soi fascinant

[Sylia]

J'ai pris le temps d'aller visiter tous les liens que vous m'avez si gentiment offert, et je vous en remercie parce que je les trouve très pertinents.

Est-ce que tu voulais dire plutôt un polygone régulier à n côtés ?

Oui, je m'excuse, c'est évidemment un polygone et non un polynôme ! Je faisais des exercices sur les ensembles de polynômes à ce moment-là, ce qui explique l'erreur

Je me suis détachée des maths (dans le sens académique) après mon bac mais j'utilise toujours le nombre d'or pour faire certaines proportions et perspectives dans mes dessins.

Bien que n'ayant jamais entendu le terme "nombre d'or" auparavant, j'ai eu une forte impression de déjà vu en lisant la formule mathématique de ce nombre. Je suis donc partie fouiner dans mes cours, et je l'ai finalement trouvé : j'ai eu l'occasion d'étudier en profondeur la suite de Fibonacci auparavant, et j'étais en effet tombée sur ce terme-là.
Après ton explication, il prend forcément une dimension tout autre à mes yeux. Je suis également intéressée par les arts puisque je dessine un peu, et faire face à l'apparition de ce nombre dans des oeuvres si connues me déroute. Si tu voulais me scotcher : c'est réussi !
Je pense lire le livre que tu m'as recommandé puisqu'il a l'air fort intéressant

"Pourquoi le monde se conforme t-il à des lois numériques et mathématiques ?"
Serait-ce plutôt : les lois numériques et mathématiques expliqueraient le monde de notre regard d'humain-e ?
Ou : Nous sommes nous inspiré-e-s de la nature pour établir ces lois numériques et mathématiques ?

Cet aspect du problème me semblait aussi possible. Evidemment, l'être humain est à l'origine de ces lois, puisqu'il a lui-même posé des axiomes qui ne peuvent être prouvés, et dont toutes les autres lois découlent. Cependant, ces axiomes sont des propriétés qui sont évidentes même sans démonstration. On ne peut pas prouver que 1+1 = 2 (ce qui d'ailleurs peut être faux en fonction de la base dans laquelle on le calcule...). Alors, les coincidences apparaissant dans les lois déduites n'ont pas pu être anticipées par l'homme. On en revient un peu au problème de "l'oeuf et la poule". On ne peut savoir qui est la cause et qui est la conséquence.

Puis pour se détendre un peu et parce que j'adore

Ces images sont vraiment hilarantes (oui, je fais partie de ces rares personnes que les maths font parfois rire ). J'en ai profité pour les enregistrer, et les partager aux connaisseurs. Au passage, cette cardioïde est réellement sublime

Quaternité, blog de Rémi Schulz, pourrait t'intéresser : il s'intéresse aux coïncidences, essentiellement numériques (nombre d'or, suites de Fibonacci, quaternité, etc.).

Je suis allée y faire un tour, et même si je n'ai encore eu le temps de tout regarder, j'ai trouvé deux/trois éléments très intéressants. Merci beaucoup

Exemple de ces phénomènes ? Gravitation (newtonienne, pas avec Einstein) et électricité statique. Les deux lois disent que deux corps sont attirés (ou repoussés) par une force proportionnelle au produit de leurs masses ou de leurs charges et inversement proportionnelle au carré de la distance qui les sépare.

J'ai beau connaitre ces deux formules depuis la nuit des temps et avoir remarqué la similitude, j'avoue ne m'être jamais arrêtée dessus.

A mon avis, d'autres avant moi y ont pensé et les petits-enfants de ceux-là sont en train de se tuer à faire émerger une théorie du tout, équation unique simplissime qui pourrait tout expliquer. Ils cherchent toujours, mais ont fait des progrès.

Lorsque je tombe sur des similitudes entre des domaines variés, je tends également à penser que cette équation magique existe peut-être. J'ai lu dans ta présentation que tu avais été impressionné par l'existence des orbitales électroniques. Ca a eu le même effet pour moi. Cette simple existence permet d'expliquer les liaisons les plus grandioses de notre univers, mais ce concept m'a fait penser à toute autre chose : les relations humaines. En effet, on observe de même des liaisons entre deux parties permettant de les rendre plus stable ou moins stable. Même si ici, le terme de stabilité n'est plus physique mais psychologique en général. C'est en soi fascinant

[Thalweg]

J'ai beau connaitre ces deux formules depuis la nuit des temps et avoir remarqué la similitude, j'avoue ne m'être jamais arrêtée dessus.

J'ai donné celles là parce que plus communes, sinon tu as l'analogie résistance électrique/chute d'eau pour lesquelles l'équation est la même (au nom des grandeurs près) ou hauteur d'eau des nappes aquifères et transfert de chaleur dans la matière solide. Et j'en passe.

Pour les orbitales, on parle bien "d'atomes crochus", non ? La stabilité en chimie est définie par l'état de moindre énergie interne, ça doit pouvoir être transposable aux relations humaines. Mais je ne me risquerai pas à faire la comparaison. Aussi, je suis presque certain que les équations décrivant les mouvements d'eau dans un canal pourraient s'appliquer aux mouvements de foules dans des rues...

Pour moi, un des principes fondamentaux est justement celui qui dit que toute entité cherchera à arriver à un état de moindre énergie. C'est pour cela que la Terre est ronde, que l'essence explose, que le soleil fusionne de l'hydrogène, et que je ne range pas ma chambre... C'est fascinant, en effet.

[TourneLune]

Aussi, je suis presque certain que les équations décrivant les mouvements d'eau dans un canal pourraient s'appliquer aux mouvements de foules dans des rues...

Ca c'est la mécanique des fluides, tout simplement, non?

[Thalweg]

Oui, c'est effectivement de la mécanique des fluides, plus précisément les équations de Navier-Stokes dans lesquelles on a négligé le terme de frottement entre particules fluides et parois. Enfin, si je me souviens bien.

[Korydween]

On ne peut pas prouver que 1+1 = 2

Petite intervention rapide pour dire que ce n'est pas tout à fait vrai. Bertrand Russel et Alfred North-Witehead ont donné une preuve logique que 1+1=2 dans Principia Mathematica.
http://math.stackexchange.com/questions ... -that-11-2

Hors-sujet

Si l'histoire de Russel et pourquoi il a tenu à prouver ceci intéresse des gens, je ne peux que conseiller le roman graphique Logicomix, qui est excellent ! 

[Malou]

De la même façon, je n'ai jamais tellement apprécié les maths dans la mesure où je n'en voyais pas l'utilité, mais l'année dernière j'ai acheté un livre La pensée de Dieu des frères Bogdanov en brocante et je me suis réellement demandée pourquoi quand on étudiait les suites, on ne nous parlait pas tout simplement de la suite de Fibonnacci, du nombre d'or, ou encore du nombre de Sommerfield ?
C'est tellement incroyable ! Littéralement, ce livre, même si par moment est un peu trop historique à mon goût, a changé ma vision des maths.

Et je m'interroge toujours à savoir pourquoi la suite de Fibonnacci régit autant notre monde ? Ce n'est certainement pas un hasard, du nombre de pétales des fleurs, aux branches de flocon, jusqu'à la proportion de nos phalanges. Est ce que les premiers mathématiciens ont crée cette suite en prenant exemple sur le monde, ou est ce que c'est les mathématiques qui appuie le monde ?

Pareillement, pour le nombre de Sommerfield, qui régit la force électromagnétique (= 1/137), j'ai lu que si un seul chiffre était remplacé la réalité s'écroulait. Qu'est ce que ça signifie concrètement ? On pourrait marcher sur les murs ?
Parfois, il m'arrive à penser que finalement, nous ne sommes que des chiffres. Après tout, nous sommes un assemblement de cellule, même un assemblement de protéine, eux même formé par des acides aminés, formés par des atomes, formés par des moles, dans cet infiniment petit, est ce que nous sommes pas simplement des chiffres ?

[Thalweg]

Si je me souviens bien, le nombre de Sommerfeld, ou constante de structure fine est un nombre sans dimensions qui relie une série de constantes physiques (constante de Planck, permittivité du vide et vitesse de la lumière). L'idée d'effondrement de la réalité est liée à l'idée que si cette constante divergeait, la fusion ne serait pas possible à l'intérieur des étoiles, et "on se retrouverait" dans un univers froid et "mort". Pareil, une différence de quelques pourcents amènerait à l'impossibilité de fusionner des atomes d'hélium en carbone, amenant l'impossibilité du développement de la vie sous la forme que nous connaissons. La réalité ne s'écroulerait probablement pas. L'humanité et la vie telle que nous la connaissons, surement. D'un autre côté, il est assez compliqué de simuler un univers ayant des constantes (et pourquoi pas des lois en fait ?) différentes de façon suffisamment fine pour voir si un processus intéressant (genre, la vie sous forme carbonée) pourrait apparaître. On manque de puissance de calcul. C'est déjà (actuellement techniquement, ou du moins il y a sept ans ça l'était, et je ne sais pas si on a avancé depuis) impossible de résoudre les équations de Schrödinger pour autre chose qu'un atome d'hydrogène, alors un univers ?

De cette idée découle ce qu'on appelle le "principe anthropique" : de la myriade d'univers existants potentiellement, différant par les valeurs des constantes physiques fondamentales, le seul univers où nous pouvons exister est celui-ci. Dans les autres, nous ne pourrions plus que probablement pas exister (d'où les guillemets sur "on se retrouverait") et donc ne pourrions pas mesurer d'autres constantes physiques. Cela dit, faute de simulations, il est assez difficile de trancher exactement.

Au niveau de "nous ne sommes que des chiffres", je me permets de t'orienter vers ce qu'on appelle l'émergence, ou comment des comportements complexes peuvent découler de règles simples. Et sinon, la Science du Disque-Monde, de Terry Pratchett (RIP), Jack Cohen et Ian Stewart. L'émergence est évoquée dans le tome 1, le principe anthropique aussi, et tout ce dont je viens de parler découle à moitié de ce bouquin (ou des deux premiers tomes, je ne sais plus exactement). Enjoy. Et je vais essayer de trouver ton bouquin aussi, ça semble sympa.

[cyclingfrog]

Bonjour

formés par des moles

Attention aux abus de langage. En tant qu'ancien prof de physique-chimie, je suis peut-être atteint de "déformation professionnelle". Mais j'estime que chaque terme a un sens précis et une utilisation adéquate du langage ne peut que contribuer à améliorer la clarté des échanges.
Nous sommes formés d'atomes, en effet, mais pas de moles. Pour rappel, la mole est une unité de quantité de matière contenant 6,02x10²³ entités identiques (c'est le fameux nombre d'Avogadro). C'est donc une unité qui permet de quantifier des entités chimiques (atomes, ions, molécules, composés ioniques). La mole n'est pas une "pièce" constitutive de la matière, elle la quantifie.
Voilà, c'est sûrement mon ancienne profession qui a rejailli en moi et qui m'a poussé à apporter ces quelques précisions.
Pour en revenir au sujet initial, il ne me semble pas surprenant que l'on retrouve régulièrement dans la nature des constantes, proportions ou autres suites. Toute la matière qui nous entoure, qu'elle soit vivante ou non, est soumise aux quatre interactions fondamentales (gravitationnelle, électromagnétique, nucléaire forte, nucléaire faible) et on peut supposer, a priori, que lorsque différents corps sont soumis à des contraintes de mêmes natures, "leurs réponses" en terme de propriétés seront semblables. En ce qui concerne les structures vivantes, le métabolisme qui les caractérise génère des problématiques énergétiques : la dépense d'énergie ne doit pas excéder la quantité susceptible d'être absorbée pour qu'il puisse y avoir survie et donc pérennisation de l'espèce. Là encore, on peut imaginer que des stratégies similaires aient été développées face à des contraintes communes.

est ce que nous sommes pas simplement des chiffres ?

La vision est certainement réductrice, mais il semble clair que la matière est modelée par différents types de contraintes engendrant des propriétés quantifiables, rendant les mathématiques indissociables du monde autour de nous. Je ne dirais pas que les mathématiques ont créé le monde, je dirais que les mathématiques permettent d'évaluer quantitativement des propriétés et des phénomènes qui sont des réponses à tous les processus physiques, chimiques et biologiques qui sont à l'oeuvre dans l'univers depuis sa formation.
Cordialement

[soazic]

Je regrette bien de ne pas être en capacité de comprendre tous vos propos mais les formes produites pas la nature sont sources de moments de fascination dont on ne se lasse pas, les fractales, les cristaux, l'élaboration lente d'une fleur, les formes symétriques parfois très complexes de certaines (passiflore, nigelle). tout cela est tellement fou.

[Thalweg]

Pour les cristaux, la plupart des formes sont liées à ce qu'on appelle les assemblages compacts, en gros la meilleure (moins volumineuse) façon d'empiler des sphères de diamètre donné (généralement de l'oxygène), les autres atomes venant se caler entre. La surface se forme selon les plans dans lesquels l'énergie de surface est la plus faible. C'est également fonction de la température, de la pression et de sûrement tout un tas d'autres variables...

Ça m'empêche pas d'adorer la cristallographie et les cristaux, de même qu'être fasciné par les fractales.

[Malou]

De cette idée découle ce qu'on appelle le "principe anthropique" : de la myriade d'univers existants potentiellement, différant par les valeurs des constantes physiques fondamentales, le seul univers où nous pouvons exister est celui-ci.

Où nous ne pouvons pas exister nous, mais (attention, naïveté absolue ^^) est-ce que ce serait possible qu'un nous différent, avec un autre métabolisme ect, existe dans ces autres univers qui sont régis par d'autres lois ? Le film Interstellar m'a un peu tourné là tête, mais après tout nous ne sommes pas encore capable d'admettre l'existence de ces autres univers (à moins par la théorie des cordes ?). Enfin, je divague et je ne connais pas suffisamment le sujet pour m'engager dedans. Seulement, sur tous les univers qui existent, ce serait quand même surprenant qu'il n'y ait de la vie que sur un seul, quand on voit que sur Terre la diversité est déjà bien développée, selon nos lois et principes.

Et je prends note du livre, je m'y plongerai plus tard, merci

Mais j'estime que chaque terme a un sens précis et une utilisation adéquate du langage ne peut que contribuer à améliorer la clarté des échanges.

L'erreur est mienne. Je ferai attention les prochaines fois.
Merci pour les éclaircissements, ça m'a ouvert d'autres voies de réflexion.

[Thalweg]

C'est pourquoi j'ai précisé : la vie "telle que nous la connaissons" ;-)

En théorie, tout est possible. On a déjà hypothétisé sur des formes de vie présentes dans le plasma à la surface des étoiles, ou à partir du silicium et d'autres trucs bizarroïdes. D'un autre côté, si une infinité d'univers existent, une partie de cette infinité doit avoir des constantes physiques équivalentes aux nôtres, et donc ressembler à celui-ci, et qui sait, peut-être voir l'apparition de la vie aussi. Mais comme j'ai dit, on n'a pas la puissance de calcul nécessaire.

Une autre possibilité est que cette univers-ci est celui qui minimise l'énergie totale, comme s'efforcent de faire tous les systèmes physiques et chimiques. Dés lors, cet univers à l'énergie minimale ne serait que le seul existant. Mais là, je théorise purement et simplement, sans sources pour me soutenir.

Hors-sujet

On en revient, au final, à cette question lancinante, dont chaque réponse est tout aussi effrayante qu'une autre : "Sommes-nous seuls dans le Multivers ?"

[Jacques Bergur]

Je me permets d’intervenir sur ce forum fort intéressant, et qui évoque des sujets qui me fascinent depuis de nombreuses années.


En ce qui concerne les « coïncidences » évoquées par Sylia et ses interlocuteurs, il me semble qu’il s’agit avant tout de la manifestation de ce que les mathématiciens appellent des isomorphismes. C’est-à-dire des identités de structures entre « mondes » très différents, on peut parler de ces isomorphismes sans utiliser de mathématiques tout en gardant une assez bonne précision dans le maniement du concept, et si cela vous intéresse, nous pourrions en discuter dans un autre post.

Il n’en reste pas moins que cette notion d’isomorphisme permet non seulement de clarifier les coïncidences de Sylia, mais aussi les identités d’équations entre plusieurs domaines de la physique, et même plus, cette notion permet de visualiser les rapports qu’il y a entre les mathématiques et le monde physique dans lequel nous sommes plongés.

Vous me pardonnerez si les notions que j’évoque dans ce post (et éventuellement les suivants ) vous sont familières et vous paraissent trop évidentes, mais je crois que parfois revenir sur des notions fondamentales permet de mieux cerner les problèmes. Alors je me lance :


La nature s’exprime en langage mathématique. Ce qu’il faut entendre par là c’est que l’on n’a pas trouvé de meilleur moyen que le langage mathématique pour exprimer les lois fondamentales monde physique. Et comme le rappelle Richard Feynman, personne ne sait pourquoi.

Bien que les Grecs aient déjà évoqués cette idée un stade embryonnaire, celui qui paraît avoir vraiment prit conscience le premier du fait que « la nature s’exprime en langage mathématique » s’appelait Galilée. D’autres ensuite ont confirmé cela bien sûrs, (Newton et tous ses collègues et successeurs).

Le langage mathématique est tellement adapté à ces lois fondamentales du monde physique, qu’il permet de les modéliser, de les conceptualiser, de relier ces concepts entre eux, de prévoir l’évolution des systèmes physiques et de les mettre à notre service.

La connaissance et la modélisation des lois physiques que le langage mathématique autorise, a permis à l’homme non seulement de découvrir des secrets de la nature, mais aussi de composer avec elle et de réaliser des choses incroyables comme s’affranchir du jour et de la nuit, s’affranchir des lois de la gravité, se parler se voir à distance, mettre au service des hommes des forces des millions de fois plus puissantes que la force animale et bien d’autres choses encore

Il n’y a pratiquement plus aucune de nos actions quotidiennes qui ne fassent appel aux miracles que cette correspondance entre mathématiques et monde physique a engendré

(Toutefois, pour autant il ne semble pas que cela rende l’homme plus heureux…)

Avant d’aborder la notion d’isomorphisme proprement dite, il est bon de noter que le langage mathématique a deux particularité stupéfiantes...

Mais bon, peut-être vaut-il mieux que j'en reste là pour aujourd’hui pour ne pas rendre cette intervention trop soporifique; mais si cela intéresse quelqu’un, je suis prêt à échanger là-dessus, car le sujet est totalement fascinant...

[Holosmos]

Il est tout de même important de noter, que ce qu'appelle Galilée les mathématiques, c'est en fait la géométrie. Le langage mathématique tel qu'on le connait n'a vraiment été construit qu'à partir de la fin du 19e siècle.

De plus, dire que la Nature se comprend dans le langage mathématique me paraît un peu facile à dire, mais dur à justifier. D'ailleurs Galilée ne dit pas que la Nature s'écrit dans le langage mathématique, il dit que pour étudier la Nature il faut la lire dans le langage mathématique (la géométrie), ce qui est assez différent. Cela peut soit signifier que par nos inaptitudes, on doit utiliser le langage mathématique. Ou alors par nécessité indépendante de nous, il faut utiliser le langage mathématique.

Je ne comprends pas l'engouement face aux isomorphismes ...

De même pour le nombre d'or ou la suite de Fibonnacci.

D'ailleurs je me permets de revenir sur ce sujet.

On lit souvent que le nombre d'or est partout. C'est tout simplement faux. On arrive à mesurer des choses semblables, mais très, très rarement le nombre d'or lui même. C'est comme si on disait qu'à chaque fois qu'on voit 3 on voit pi ... c'est un peu ridicule.

Pour ce qui est du lien avec l'art, c'est par définition même du nombre qu'il remplit ses qualités, rien de très étonnant donc.

Ensuite, on retrouve ce nombre dans les équations (formellement, donc) parce que la suite de Fibonnacci est un système dynamique extrêmement simple. Et comme tout système très simple, on s'y ramène ou on le rencontre facilement.

Ce n'est donc pas un hasard, ou une loi de la nature. Juste un fait : les choses simples, sont simples, et sont plus souvent utilisées que les autres.

[Jacques Bergur]

Il est tout de même important de noter, que ce qu'appelle Galilée les mathématiques, c'est en fait la géométrie. Le langage mathématique tel qu'on le connait n'a vraiment été construit qu'à partir de la fin du 19e siècle.

De plus, dire que la Nature se comprend dans le langage mathématique me paraît un peu facile à dire, mais dur à justifier. D'ailleurs Galilée ne dit pas que la Nature s'écrit dans le langage mathématique, il dit que pour étudier la Nature il faut la lire dans le langage mathématique (la géométrie), ce qui est assez différent. Cela peut soit signifier que par nos inaptitudes, on doit utiliser le langage mathématique. Ou alors par nécessité indépendante de nous, il faut utiliser le langage mathématique.

Je ne comprends pas l'engouement face aux isomorphismes ...

De même pour le nombre d'or ou la suite de Fibonnacci.

D'ailleurs je me permets de revenir sur ce sujet.

On lit souvent que le nombre d'or est partout. C'est tout simplement faux. On arrive à mesurer des choses semblables, mais très, très rarement le nombre d'or lui même. C'est comme si on disait qu'à chaque fois qu'on voit 3 on voit pi ... c'est un peu ridicule.

Pour ce qui est du lien avec l'art, c'est par définition même du nombre qu'il remplit ses qualités, rien de très étonnant donc.

Ensuite, on retrouve ce nombre dans les équations (formellement, donc) parce que la suite de Fibonnacci est un système dynamique extrêmement simple. Et comme tout système très simple, on s'y ramène ou on le rencontre facilement.

Ce n'est donc pas un hasard, ou une loi de la nature. Juste un fait : les choses simples, sont simples, et sont plus souvent utilisées que les autres.

Je suis entièrement d'accord avec toi en ce qui concerne le nombre d'or.

Si il est vrai que Galilée a dit que la nature se lit en langage mathématiques, toute la kyrielle de savant qui ont fondé la physique ont conclu que les mathématiques étaient le langage de la nature, ou tout au moins celui des lois de la physique (et ça c'est pas moi qui le dit mais Newton, Laplace,Maxwell, Einstein, Boltzman, Planck, Dirac, Schrödinger, Feynman, Penrose et tous les autres). Et la justification est que seul ce langage a permis de prévoir, composer, et mettre à notre service les lois de la nature (pas un jour sans que nous utilisions ces lois: radio, télé, avions, médecine, chimie,électricité).

Ton hypothèse que "par nécessité indépendante de nous, il faut utiliser le langage mathématique" me parait d'ailleurs compatible avec tout cela.

Cela a conduit plusieurs de ces savants à se poser la question du Platonisme Mathématique (mais c'est un autre sujet).

Quant aux isomorphismes (notion très précise en mathématiques), ils sont l'un de des concepts miraculeux de ce langage...

[Holosmos]

Si il est vrai que Galilée a dit que la nature se lit en langage mathématiques, toute la kyrielle de savant qui ont fondé la physique ont conclu que les mathématiques étaient le langage de la nature, ou tout au moins celui des lois de la physique (et ça c'est pas moi qui le dit mais Newton, Laplace,Maxwell, Einstein, Boltzman, Planck, Dirac, Schrödinger, Feynman, Penrose et tous les autres). Et la justification est que seul ce langage a permis de prévoir, composer, et mettre à notre service les lois de la nature (pas un jour sans que nous utilisions ces lois: radio, télé, avions, médecine, chimie,électricité).

Ton hypothèse que "par nécessité indépendante de nous, il faut utiliser le langage mathématique" me parait d'ailleurs compatible avec tout cela.

Je n'ai pas dit que c'était faux. Je dis que c'est difficile à justifier ... alors que c'est la justification qui compte dans de telles questions.

Quant aux isomorphismes (notion très précise en mathématiques), ils sont l'un de des concepts miraculeux de ce langage...

Je connais cette notion mais je ne vois toujours pas le rapport. Tu peux m'éclairer ?

[Jacques Bergur]

Si il est vrai que Galilée a dit que la nature se lit en langage mathématiques, toute la kyrielle de savant qui ont fondé la physique ont conclu que les mathématiques étaient le langage de la nature, ou tout au moins celui des lois de la physique (et ça c'est pas moi qui le dit mais Newton, Laplace,Maxwell, Einstein, Boltzman, Planck, Dirac, Schrödinger, Feynman, Penrose et tous les autres). Et la justification est que seul ce langage a permis de prévoir, composer, et mettre à notre service les lois de la nature (pas un jour sans que nous utilisions ces lois: radio, télé, avions, médecine, chimie,électricité).

Ton hypothèse que "par nécessité indépendante de nous, il faut utiliser le langage mathématique" me parait d'ailleurs compatible avec tout cela.

Je n'ai pas dit que c'était faux. Je dis que c'est difficile à justifier ... alors que c'est la justification qui compte dans de telles questions.

Quant aux isomorphismes (notion très précise en mathématiques), ils sont l'un de des concepts miraculeux de ce langage...

Je connais cette notion mais je ne vois toujours pas le rapport. Tu peux m'éclairer ?

C’est un peu long à expliquer, surtout en termes non mathématiques, c’est pour ça que j’ai écrit là-dessus un bouquin sous forme de thriller destiné aux non-scientifiques, tout comme aux scientifiques.

Mais puisqu’il s’agit de répondre, cher Holosmos, à ta question de matheux, je demande aux non -matheux de me pardonner ce post.

Donc pour Holosmos et pour faire (très, très) court :
Les isomorphismes permettent de résoudre des problèmes qui se posent dans un « monde », en raisonnant sur les objets d’un « autre monde » qui n’a en fait rien à voir avec le premier, mais qui a exactement la même structure. En d’autres termes, un isomorphisme est un « simulateur parfait ».

Exemples :

-On peut travailler sur l’ensemble des vecteurs de l’espace euclidien qui sont des êtres géométriques, en raisonnant sur RxRxR (êtres algébriques).
-On peut travailler sur la géométrie du plan, en raisonnant sur Z

Autre aspect isomorphique :
-On peut raisonner sur les oscillateurs mécaniques, en utilisant des équations différentielles qui sont les mêmes que celles qui permettent d’étudier les oscillateurs électriques.

Mais on peut trouver d'autres isomorphismes fascinants, non mathématiques, et permettant d’expliquer des comportements spécifiques aux humains.

Encore une fois je pense qu’il n’est pas souhaitable de s’enfermer dans une discussion trop spécialisée destinée aux matheux. Donc promis : je le ferai plus.

Si le sujet évoqué dans le poste précédent intéresse du monde, on peut aborder ce sujet captivant dans un langage de tous les jours. C’est plus sympa mais c’est plus long…

[Holosmos]

En fait c'est là où je ne suis pas d'accord. Les mathématiques, depuis la révolution moderne, n'étudient plus les objets pour eux mais les relations entre objets mathématique. Un isomorphisme s'inscrit alors très naturellement dans cette optique.

Il ne s'agit donc plus de raisonner sur des objets et de se rendre compte de leur similarité avec d'autres, mais de considérer les relations et de les appliquer à certains objets.
D'ailleurs, il me semble étrange de qualifier deux « mondes » isomorphes de sans rapport l'un avec l'autre. L'isomorphisme montrant justement que ces deux mondes sont en relation étroite.

L'exemple de la géométrie est intéressant. Depuis les résultats de Sophus Lie, on sait que pour étudier une géométrie (par exemple euclidienne ou hyperbolique), il faut étudier son groupe d'automorphismes. On se ramène bien à l'étude de relations et non de cas disjoints.

[madeleine]

D'ailleurs, il me semble étrange de qualifier deux « mondes » isomorphes de sans rapport l'un avec l'autre. L'isomorphisme montrant justement que ces deux mondes sont en relation étroite.

Mais quel genre de relation, justement ? Et sur quel plan ? Peut-on vraiment en tirer quelque chose ?
(Pas besoin d'être matheuse pour être curieuse désolée si ma question est naïve, j'aime bien les maths mais j'ai le niveau éclectique ...)

[Holosmos]

Bah la relation c'est l'isomorphisme lui-même . Il faut juste bien comprendre qu'on invente pas un isomorphisme, il a toujours été là.

C'est d'ailleurs pas du tout anodin un isomorphisme. C'est extrêmement contraignant comme relation. Donc dire qu'on a relié deux mondes qui n'ont rien à voir l'un avec l'autre .... je suis pas d'accord. On peut à la limite dire qu'on a cru qu'ils avaient rien à voir l'un avec l'autre, mais une fois qu'on a un isomorphisme on ne devrait plus le dire.