[QALC] Question pour nos éminents mathématiciens

[Youpla]

Je ne comprends toujours pas.
En cherchant un plus grand réel juste en-dessous de 1, c'est un peu comme si tu tentais de les énumérer (les réels) et c'est impossible. Ce serait alors le 1er juste en-dessous de 1 et il y en aurait un 2ème juste en-dessous et ainsi de suite.
La continuité même des réels fait qu'on pourra toujours en trouver un autre entre deux distincts, donc pas possible de trouver un plus grand qui [mettre ce qu'on veut ici].

[Swinn]

merci de ta réponse youpla
si je comprends bien ce que tu me dis, ce nombre que je cherche non seulement n'existe pas mais en plus ne peut pas exister c'est ça?

[Pataboul]

Swinn j'essayais surtout de présenter ma façon de me représenter l'infini qui permet de se figurer pourquoi il n'existe pas de nombre infiniment proche de l'infini.

Formulé plus classiquement:
Le nombre que tu cherche est infiniment proche de 1, donc il vaut 1-(1/∞) or 1/∞=0 donc ton nombre vaut 1.
Je rejoins Youpla, ce nombre ne peut pas exister. De même que lorsque je me projette à l'infini rien d'autre que l'infini ne peut m'entourer.

[Youpla]

C'est tout à fait ça !
Mais je peux me tromper...

Edit : j'ai posté en même temps que Pataboul.

[Fu]

J'ai regardé la vidéo (0,9999… = 1) et, tout comme le titre me le laissait entendre, c'est du caca. Quand il dit à 5'57 que la suite 0,9 + 0,09 + 0,009… à l'infini est exactement égale à un, c'est une ânerie monumentale. Il s'agit de la suite :



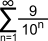
Celle-ci tend vers 1 mais n'y arrivera jamais. Par définition, elle prend 90% de la distance à 1 et l'ajoute à la somme. Donc par définition, il restera toujours 10% de cette distance, cette dernière finira par être infiniment petite mais ne disparaîtra par pour autant, c'est le fameux espace qui te paraît manquant dans la continuité, et qui ne manque pas du tout.

La démonstration proposée par le gars est fallacieuse, elle utilise des valeurs intermédiaires numériques et colporte donc des approximations qui mènent à l'erreur. Par exemple quand on utilise la valeur ⅓ dans un calcul, on ne peut pas écrire 0,333333… parce que 3 × 0,333333… semble valoir 0,999999…, uniquement parce que l'écriture des nombres est (forcément) incomplète. À la place, faites 3 × ⅓ et vous aurez le bon résultat.

Ce n'est pas pour rien que les fractions et les suites ont été créées.

[Pataboul]

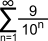
"Celle-ci tend vers 1 mais n'y arrivera jamais." De même qu'on n'arrive jamais à l'infini. Mais si on arrivait à l'infini, on arriverait aussi à 1.

[Fu]

La formule utilisée de la vidéo dit que dans tous les cas il reste 10% de la distance à 1. Mettons que tu arrives à l'infini, en oubliant que c'est impossible par définition. Ben il reste encore un peu de distance à 1, 10% de la précédente itération (l'itération numéro « infini - 1 »), c'est la formule qui veut ça, et ça prouve que quand tu crois être à l'infini ben tu n'y es pas vraiment, puisque c'est impossible.

Le concept d'arriver à l'infini explose dès qu'on se demande ce qu'il y a au-delà, n'en déplaise à Buzz Lightyear. Explorez mentalement le fin fond de l'espace, avancez à une vitesse incroyable, pendant des heures s'il le faut, essayez de visualiser ce que c'est que d'arriver à l'infini ; à chaque fois que vous arrivez face à un mur avec marqué « infini » dessus, détruisez-le et contemplez l'infini, le vrai, qui s'étend au-delà. En maths, c'est pareil. Si vous y êtes, c'est que vous n'y êtes pas.

[Youpla]

Le concept d'arriver à l'infini explose dès qu'on se demande ce qu'il y a au-delà, n'en déplaise à Buzz Lightyear. Explorez mentalement le fin fond de l'espace, avancez à une vitesse incroyable, pendant des heures s'il le faut, essayez de visualiser ce que c'est que d'arriver à l'infini ; à chaque fois que vous arrivez face à un mur avec marqué « infini » dessus, détruisez-le et contemplez l'infini, le vrai, qui s'étend au-delà. En maths, c'est pareil. Si vous y êtes, c'est que vous n'y êtes pas.

C'est bien pour ça que des 9 à l'infini, ça ne s'arrête jamais et qu'il n'y a donc pas d'interstice ou d'erreur (ou appelez ça comme vous voulez) entre 0,99999 (à l'infini) et 1. Il n'y a pas d'arrêt à un moment donné, ce n'est pas une approximation à 10 puissance -n près, quelque soit ce n.

[Jahroo]

Puisque :
0,999999999999999999999....................développé à l'infini est strictement égal à 1,

Quel est le plus grand chiffre possible qui soit immédiatement et strictement inférieur à 1 ?

Comment peut-on définir un chiffre rationnel ou irrationnel tout en se référant à l'infini? Cela ne revient-il pas à chercher une limite valable dans l'absolu?

N'est-il pas cohérent qu'en ce point (l'infini) la logique commune n'ai plus cours et que l'absurde soit de mise?

Je te remercie par ailleurs pour cette égalité incongrue que je ne connaissais pas et qui vient rappeler la qualité relative du Savoir.

edit de forme

[Swinn]

Swinn j'essayais surtout de présenter ma façon de me représenter l'infini qui permet de se figurer pourquoi il n'existe pas de nombre infiniment proche de l'infini.

Formulé plus classiquement:
Le nombre que tu cherche est infiniment proche de 1, donc il vaut 1-(1/∞) or 1/∞=0 donc ton nombre vaut 1.
Je rejoins Youpla, ce nombre ne peut pas exister. De même que lorsque je me projette à l'infini rien d'autre que l'infini ne peut m'entourer.

magnifique Pataboul ! ta démonstration est parfaite et répond totalement à ma question initiale.

Sinon fu, tant qu'il te reste un peu de distance infiniment petite soit elle tu n'es pas encore à l'infini (tu ne fais qu'y tendre), si tu rajoute une distance supplémentaire ce rajout va modifier ta distance même de façon infinitésimale.

Tu ne "rentres" pas dans l'infini une fois franchi un autre seuil car effectivement ce seuil n'existe pas. l'infini serait comme un monde parallèle qui obéit à ses propres lois dans lequel nos lois n'ont pas cours mais qui influence malgré tout notre monde.

Pour dire autrement, si tu ajoutes 1 à un nombre infiniment grand tu obtiens un nombre plus grand encore. si ce nombre tu le mets en exponentiation de lui même un nombre infini de fois tu obtiendras un nombre encore plus grand et ainsi de suite.

le calcul avec les nombres infinis, plus exactement les nombres transfinis n'obéissent pas aux mêmes règles. Cantor a nommé ces nombres Aleph.
Aleph +1 =Aleph, Aleph+Aleph=Aleph ,Aleph x Aleph =Aleph et ainsi de suite.
C'est un calcul qui va au dela de la notion de limite.

[Pataboul]

La formule utilisée de la vidéo dit que dans tous les cas il reste 10% de la distance à 1. Mettons que tu arrives à l'infini, en oubliant que c'est impossible par définition. Ben il reste encore un peu de distance à 1, 10% de la précédente itération (l'itération numéro « infini - 1 »), c'est la formule qui veut ça, et ça prouve que quand tu crois être à l'infini ben tu n'y es pas vraiment, puisque c'est impossible.

Le concept d'arriver à l'infini explose dès qu'on se demande ce qu'il y a au-delà, n'en déplaise à Buzz Lightyear. Explorez mentalement le fin fond de l'espace, avancez à une vitesse incroyable, pendant des heures s'il le faut, essayez de visualiser ce que c'est que d'arriver à l'infini ; à chaque fois que vous arrivez face à un mur avec marqué « infini » dessus, détruisez-le et contemplez l'infini, le vrai, qui s'étend au-delà. En maths, c'est pareil. Si vous y êtes, c'est que vous n'y êtes pas.

Le truc c'est de prendre le problème à l'envers. Considérons nous à l'infini et voyons ce qu'il se passe, coûte que coûte. Et là comme Swinn l'a dit c'est un genre d'autre dimension, il se passe des truc très étranges mais logiques dans cet univers virtuel des nombres.

Reprenons ton image du mur, si quand tu le casse il reste autre chose derrière c'est que ce n'est pas le bon, l'affiche était mensongère mais ça dis juste que vouloir aller à l'infini en marchant ou avec des réacteurs ne sert à rien: téléport et le problème est réglé! C'est des maths, on a le droit et en plus c'est infaillible. T'es donc devant le vrai mur du vrai infini,sans doutes possibles. Si tu le casse tu te retrouve non pas devant un espace vide ni d'autres murs, mais devant le même mur, parce que sinon ça voudrait dire que le mur d'avant était pas le vrai mur du vrai infini. Il ne faut pas chercher à réfléchir comme d'habitude, y'a une rupture entre l'infini et le reste du monde, c'est une sorte de bulle dans une autre dimension, une bulle ou toutes les dimensions sont confondues en un seul point en quelque sorte. Et si on arrive à se le figurer comme ça, alors les formules de Swinn ne sont pas surprenantes, voir évidentes.

[pixelvois]

Mais l'infini n'est justement pas un mur... plutôt un trou noir : si tu t'y téléportes, ben en fait tu ne finiras jamais de te téléporter 'tu te téléportera indéfiniment, fût-ce instantanément), tu auras disparu de ton point de départ, et n'apparaîtra jamais ailleurs, disparu dans le trou noir de l'infini ^^

[Pataboul]

Visualise le comme tu veux, mais seule ton imagination te limite. On ne parle pas du monde physique mais de celui des nombres.
La représentation qui me semble la plus juste est celle d'un point unique, parfaitement localisable dans l'univers aux coordonnée de "l'infini" "-l'infini" ou de n'importe quel nombre dans le cas d'une suite, mais pourtant c'est un point où il n'y a que ce point autour de lui même, en fait il n'y a plus d'autour tangible même si l'univers existe et inclus l'infini. Bref ça reviens à imaginer l'inimaginable.

Un mur c'est pas une super métaphore mais c'est toujours plus utilisable qu'un trou noir: on est même pas obligé de forcer pour passer ou regarder à travers, les portes et fenêtres sont autorisées, elles seront les métaphores des opérations mathématiques. Et elle donneront toujours sur le mur qui les portes!


[mention]Swinn[/mention] Tu sais comment les mathématiciens gèrent des opérations telles que Aleph+Aleph-Aleph? Dans ce cas l'ordre change le résultat... Ca m'a l'air un peu dangereux à manipuler ces nombres.

[Swinn]

Cantor ne détermine que 3 opérations possibles avec les transfinis, l'addition la multiplication et l'exponentiation. La soustraction pas plus que la division n'en fait partie. Donc lorsque tes opérations finissent par Aleph-Aleph (comme dans ton exemple ci dessus) ou bien Aleph/Aleph le résultat en est indéterminable, ce qui est logique puisque Aleph n'ayant pas de taille en soi, les diviser ou les soustraire revient à les comparer ce qui n'est pas possible.

L'ordre des opération avec les transfinis change le résultat mais il faut que je recherche dans ma bibliothèque en quoi précisément.

Ce fil c'est du bonheur absolu !

[dani]

Puisque :
0,999999999999999999999....................développé à l'infini est strictement égal à 1,

Quel est le plus grand chiffre possible qui soit immédiatement et strictement inférieur à 1 ?

Ce fil est passionnant, et pourtant je ne suis absolument pas mathématicienne (j'ai mis d'ailleurs plusieurs jours à me décider à le lire, je n'ai jamais pensé que j'y prendrais ce plaisir, merci à vous !).

En vous lisant hier soir, un truc me chiffonnait : pour moi 0,9999999999999999999....., même à l'infini, n'est pas égal à 1 (c'est juste par commodité que dans la vie réelle on le met égal à 1). Puis ensuite, les développements amenés, tout étant extrêmement intéressants, n'ont pas réellement répondu à la question de Swinn, ce qui m'a semblé bizarre.

Ainsi, je me suis demandée si l'assertion de Swinn n'était pas erronée à la base, ce qu'il dit d'ailleurs en quelque sorte plus haut en parlant de "monde parallèle" :

Tu ne "rentres" pas dans l'infini une fois franchi un autre seuil car effectivement ce seuil n'existe pas. l'infini serait comme un monde parallèle qui obéit à ses propres lois dans lequel nos lois n'ont pas cours mais qui influence malgré tout notre monde.

Je passais pour toute autre chose chez mon libraire il y a quelques instants, et mon regard s'est posé en flânant sur l'ouvrage de Alain Conne (mathématicien, médaille d'or du CNRS et titulaire de la chaire Analyse et Géométrie du collège de France) "la géométrie et le quantique".

Je n'ai peut-être pas bien compris (et je ferais peut-être bien mieux de me taire.. mais bon, qui ne risque rien n'a rien), mais je vous livre un bout de son texte qui éclaire bien le problème de Swinn et le règle en partie :

Contenu caché

Vous devez être inscrit et connecté sur ce forum pour voir le contenu caché.

Résumé de son petit livre (un bijou me semble-t-il) :

"En 1637, Descartes révolutionne la manière que l'on a de faire de la géométrie : en associant à chaque point de l'espace trois coordonnées, il pose les bases de la géométrie algébrique. Cette géométrie est dite " commutative " : le produit de deux quantités ne dépend pas de l'ordre des termes, et A × B = B × A. Cette propriété est fondamentale, l'ensemble de l'édifice mathématique en dépend.
Mais au début du XXe siècle, la découverte du monde quantique vient tout bouleverser. L'espace géométrique des états d'un système microscopique, un atome par exemple, s'enrichit de nouvelles propriétés, qui ne commutent plus. Il faut donc adapter l'ensemble des outils mathématiques. Cette nouvelle géométrie, dite " non commutative ", devenue essentielle à la recherche en physique, a été développée par Alain Connes"

[Invité]

Hors-sujet

Je préfère tagger HS, car ce n'est pas exactement le sujet. Mais précision, je parle bien uniquement du domaine mathématique.

Une question : est ce que pour que quelque chose existe, il ne faut pas être capable de le voir, de le citer, de l'écrire ..... etc ?

Dans le sens ou, l'infini, pourquoi existerait-il ?

On ne peut pas écrire un nombre à l'infini , même 0.9999..... (on aurait pas assez d'encre.)
On ne peut pas citer un nombre à l'infini. (on serait mort avant)

A la limite on va l'écrire : ∞ . Mais même en écrivant comme ça, l'infini est fini.

Du coup l'infini pourrait être le maximum de chiffres à la suite que l'on serait capable d'énumérés.
On pourrait dire que, si on s'arrête, c'est fini: oui en effet. Mais le but de l'infini c'est de ne pas savoir ou cela fini, or on ne peut pas aller jusque la, nous aurons toujours des nombres finis.

Ptite pensée du jour, bonjour.

[Swinn]

Non [mention]Opsiala[/mention] encore une fois l'infini n'est pas quelque chose de pensable, dès que tu penses l'infini il devient fini.
On confond fréquemment l'infiniment grand ( ou petit) qui peut toujours augmenter, en y rajouter 1 par exemple et l'INFINI mathématique qui lui ne s'augmente pas. 1 plus INFINI donne INFINI, INFINI x par INFINI donne INFINI, INFINI puissance INFINI donne également infini.
C'est pour cela qu'on a parlé de monde parallèle et de non commutativité, à savoir que le monde parallèle dicte certaines lois à notre monde, mais que aucune des lois de notre monde peuvent dicter quoique ce soit à l'infini. Il n'y a pas de réciprocité entre les 2.

La question que tu poses est la grande classique des mathématiciens, est ce que le monde mathématique préexiste et que les mathématiciens sont des découvreurs (attitude platoniste) ou bien est ce que les mathématiciens bâtissent le monde qu'ils découvrent et sont des créateurs.
D'après ce que j'ai pu lire on pencherait plutôt vers une attitude platoniste, les mathématique préexistant au monde voir que TOUT est mathématique même l'existence de l'univers en soi.

Néanmoins les infinis ont été découverts par Cantor, ils les a démontré et ils existent.

[Invité]

Non @Opsiala encore une fois l'infini n'est pas quelque chose de pensable, dès que tu penses l'infini il devient fini.
On confond fréquemment l'infiniment grand ( ou petit) qui peut toujours augmenter, en y rajouter 1 par exemple et l'INFINI mathématique qui lui ne s'augmente pas. 1 plus INFINI donne INFINI, INFINI x par INFINI donne INFINI, INFINI puissance INFINI donne également infini.
C'est pour cela qu'on a parlé de monde parallèle et de non commutativité, à savoir que le monde parallèle dicte certaines lois à notre monde, mais que aucune des lois de notre monde peuvent dicter quoique ce soit à l'infini. Il n'y a pas de réciprocité entre les 2.

@Swinn , je ne savais vraiment comment t'aborder par rapport à cette phrase (surtout qu'une phrase sur internet peut-être interprété de mille et une façon, et parfois même, pas la manière dont l'interlocuteur voudrais qu'elle soit perçu) mais commencer par NON OPSIALA, j'ai pas kiffé ^^

J'ai aucun problème à ce que tu ne sois pas d'accord avec moi, au contraire, ça ouvre le champs des possible (dédicace à Bernard Werber, mon auteur préféré )

Malgré tout je suis d'accord avec ta phrase. Cependant, si ce n'est pas "pensable" c'est abstrait. Donc ok les mathématiques peuvent être abstrait mais ils sont avant tout scientifique.
Concernant par ex, le 1+l'infini. Au final, tu as deux choix. 1+l'infini peut être égal à l'infini + 1 (pensée scientifique) et 1 + l'infini peut être égal à l'infini. (pensée abstraite)

La question que tu poses est la grande classique des mathématiciens, est ce que le monde mathématique préexiste et que les mathématiciens sont des découvreurs (attitude platoniste) ou bien est ce que les mathématiciens bâtissent le monde qu'ils découvrent et sont des créateurs.
D'après ce que j'ai pu lire on pencherait plutôt vers une attitude platoniste, les mathématique préexistant au monde voir que TOUT est mathématique même l'existence de l'univers en soi.

Néanmoins les infinis ont été découverts par Cantor, ils les a démontré et ils existent.

Par rapport à ce point, je ne suis pas dans la même optique que toi.
Je ne pense pas que les mathématiques existaient avant nous. Je pense seulement que nous avons créé les mathématiques pour avoir une notion de valeurs, grandeur, calculs.


Je vais allez voir ce que raconte Cantor, parce que si il a démontré que les infinis existent, je veux les voir

Tout ceci n'est qu'un avis, je n'ai pas de grande connaissance en mathématiques, j'avais juste envie de donner l'avis d'un néophyte

[Swinn]

Le fait que je commence par Non Opsiala signifie que directement je ne suis pas d'accord avec ce que tu dis. Par ailleurs j'ai beaucoup insisté dans ce fil que l'infini n'était, quelque soit la façon à laquelle on le conceptualise, quelque chose de pensable avec les réflexes classiques de réflexion et que l'intuition ou l'avis n' avait pas sa place .

[mention]Opsiala[/mention] tu as écrit :
Malgré tout je suis d'accord avec ta phrase. Cependant, si ce n'est pas "pensable" c'est abstrait. Donc ok les mathématiques peuvent être abstrait mais ils sont avant tout scientifique.
Concernant par ex, le 1+l'infini. Au final, tu as deux choix. 1+l'infini peut être égal à l'infini + 1 (pensée scientifique) et 1 + l'infini peut être égal à l'infini. (pensée abstraite)

Non encore une fois il n'y a pas de choix possible, les calculs sur l'infini ont été prouvés démontrés et en aucun ils offrent un choix entre une pensée abstraite ou scientifique ce qui, pour moi ne signifie pas grand chose dans notre contexte.

Les raisonnement mathématiques et logiques de Cantor, ne se préoccupent ni d'avis ni d'opinion, ni ce qu'on pense. ils ont été formellement et indiscutablement démontrés et ce n'est certainement pas moi, néophyte parmi les néophytes qui se permettrais de penser avoir les moyens de les contester voir de les réfuter.

[Invité]

Bon, je voulais juste donner mon opinion, apparemment je n'aurai pas du.

Je ne réfute absolument pas les dires de Cantor mais mon avis, mon opinion, même si à t'entendre , je n'ai pas le droit de les exprimer dans ce fil, c'est que même ce gentil monsieur s'appuie sur des choses que l'humains à créer lui même. Ce qui reviens à notre pensée déjà divergente sur le sujet.

[mention]Swinn[/mention] Les raisonnement mathématiques et logiques de Cantor
du coup, comme d'autre, enfin j'espère, je vais aller voir son histoire parce que ça m'intéresse.

Et encore une fois, je n'ai jamais dis que je détenais la vérité, bien loin de la, mais ta fermeture de dialogue ne m'incitera plus à répondre.
C'était plus des axes de discussions qu'une vérité absolu, pour exprimer un point de vue. (qui à la base n'était même pas le sujet, bref ça m'apprendra)

[Proxima]

Puisque :
0,999999999999999999999....................développé à l'infini est strictement égal à 1,

Quel est le plus grand chiffre possible qui soit immédiatement et strictement inférieur à 1 ?

Je pense que ta question ne peut par avoir de réponse car le postula de ta 1ère affirmation (égalité entre un nombre ordinal et un nombre cardinal), n'est pas repris dans ta question (à partir de quand un nombre ordinal n'est plus égal à un nombre cardinal ?) C'est à dire que ton affirmation et ta question reposent sur 2 postulats différents, qui ne sont donc pas conciliables. C'est soit une faille de raisonnement, soit une mauvais formulation.

Tu peux néanmoins user de subtilités pour passer de l'un à l'autre.
Si tu considères que 1/9=0.[1], alors tu peux considérer que 9 x (1/9)=0.[9] ET également que 9 x (1/9)=1, les deux sont identiques.

Si on devait répondre à ta question qui repose sur une erreur de perception, la réponse serait tout aussi absurde : 1-(1-(9 x (1/9)) )
ce qui ne t'aide pas d'avantage

[Swinn]

Proxima, je ne vois pas très bien bien ce que viens faire ici l'apparition des nombres ordinaux et cardinaux, il me semble plutôt que comme à ton habitude, les erreurs de perception c'est toi qui les produis.
Je pense par ailleurs que ici Pataboul, avec l'appui de Youpla a parfaitement répondu à ma question. Relire attentivement l'ensemble du fil t'aidera certainement à comprendre pourquoi et comment.

[Pataboul]

Après cette discussion y'a un point qui m'intrigue: pourquoi est-il "interdit" de soustraire ou diviser l'infini?
Certes les opérations se comportent étrangement, mais c'est déjà le cas de l'addition et la multiplication. Qu'est-ce qui fait que l'un est accepté et pas l'autre?

Cantor ne détermine que 3 opérations possibles avec les transfinis, l'addition la multiplication et l'exponentiation. La soustraction pas plus que la division n'en fait partie. Donc lorsque tes opérations finissent par Aleph-Aleph (comme dans ton exemple ci dessus) ou bien Aleph/Aleph le résultat en est indéterminable, ce qui est logique puisque Aleph n'ayant pas de taille en soi, les diviser ou les soustraire revient à les comparer ce qui n'est pas possible.

L'ordre des opération avec les transfinis change le résultat mais il faut que je recherche dans ma bibliothèque en quoi précisément.

Ce fil c'est du bonheur absolu !

Cette explication ne me parle pas du tout. S'il n'y a pas d'erreur, alors je ne comprend pas ce que tu signifie par "pas de taille en soi". La façon évidente que j'ai de le comprendre ne me pose pas plus (ou autant!) de soucis quelles que soient les opérations.

[Youpla]

Si INFINI est un nombre infiniment grand, alors INFINI + INFINI c'est "juste" ajouter deux nombres infiniment grands, on obtient un nombre infiniment grand, on n'a pas besoin de considération plus poussée. C'est une généralisation de la somme de deux nombres positifs, on obtient un nombre positif plus grand que les deux termes.
La multiplication n'est qu'une généralisation de l'addition, on fonctionne de la même manière.

La soustraction et la division impose de savoir quel infini est le plus grand pour pouvoir conclure.
Quand on soustrait des nombres finis tous deux positifs, plusieurs cas de figures peuvent apparaître, selon que le 1er terme est plus petit ou plus grand que le 2ème. On peut obtenir un nombre positif, un nombre négatif, zéro...
On compare les deux termes afin de conclure. Pour la division, c'est la même chose, il faudrait comparer le numérateur et le dénominateur.

► Afficher le texte

J'ajoute une considération toute intuitive et non rigoureuse, non sourcée, juste avec mon instinct donc.
Pour INFINI, dans le meilleur des cas, on pourrait décider que INFINI - INFINI = 0 et INFINI/INFINI = 1.
MAIS cela impliquerait que INFINI est un nombre fixé et fini, puisqu'on aurait deux nombres strictement égaux.
INFINI est le "vrai" infini, inatteignable...
Pour moi, INFINI est un nombre mouvant. Un nombre toujours en train d'augmenter...

[Swinn]

Cette explication ne me parle pas du tout. S'il n'y a pas d'erreur, alors je ne comprend pas ce que tu signifie par "pas de taille en soi". La façon évidente que j'ai de le comprendre ne me pose pas plus (ou autant!) de soucis quelles que soient les opérations.

Si tu reprends la comparaison que tu as faites plus haut disant que tu considère l'infini comme un point d'une taille infini mais non dénombrable.
Si tu additionnes 1 point + 1 point cela te donne un point de taille infini mais non dénombrable.

Mais si tu soustrais un point de taille infini et non dénombrable à un point de taille infinie mais non dénombrable que te reste t 'il sinon une quantité non quantifiable ?

C'est en cela que la soustraction ou la division ne fonctionne pas avec ce genre de nombres.