Je lance donc dans un petit topic de vulgarisation mathématique, afin d'éclaircir un peu ces "gros mots" !!
Je précise que je ne suis pas très matheuse, je travaille simplement avec ce type de tests. Donc n'hésitez pas à me faire remarquer mes probables erreurs et imprécisions, à reformuler, à enrichir... merci !
Tout d'abord un petit lexique de termes équivalents, qui suffira déjà à répondre à quelques interrogations :Centile (c)= percentile (p) = rang percentile (en gros !)
Ecart-type (ET) = racine carrée de la variance = Déviation Standard (DS) = Standard Deviation (SD), aussi représenté par la lettre sigma.
Courbe de Gauss = Courbe en cloche = courbe en chapeau de gendarme.
Ensuite, pour une conversion entre score de QI - écart-type - rang percentile, je vous renvoie à ce tableau qui résume très bien : http://les-tribulations-dun-petit-###pigeon lévitant en posture du courlis### ... ore-de-qi/
Et pour ceux qui voudraient savoir d'où ça sort, tout ça...
Dans la plupart des cas, lorsque on mesure un phénomène soumis au hasard à de nombreuses reprises ou à plein d'endroits différents, globalement les mesures obtenues seront "massées" autour d'une moyenne. Exemple : taille des hommes adultes, nombre de petits pois trouvés dans une gousse, résultat d'un lancer de deux dés...
Plus on s'éloignera de cette moyenne, moins on trouvera d'occurrences (pas beaucoup d'hommes mesurant 1m46, ni de gousses à 15 petits pois, etc.). En fait, plus on fera d'essais, plus la répartition des résultats s'approchera d'une magnifique courbe en cloche, baptisée courbe de Gauss. Celle-ci sera simplement plus ou "haute", plus ou moins "large" (c'est-à-dire que la gamme des résultats sera plus ou moins étendue, mais on retrouvera toujours cette forme).

C'est le cas de l'intelligence humaine, enfin du fameux "facteur G", lorsqu'il est mesuré par des tests.
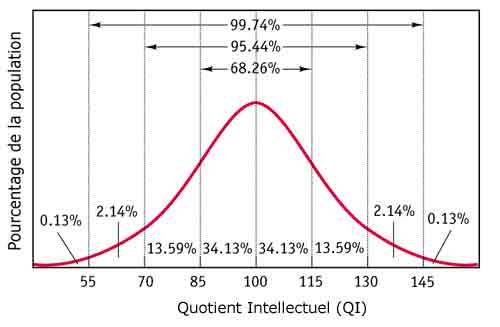
Cette représentation graphique est bien pratique puisqu'en regardant l'aire sous la courbe, on estime à peu près l'étendue de la population qui a obtenu plus ou moins que notre résultat. Mais ça reste de l'à-peu-près tant qu'on n'a pas mis tous les petits chiffres autour, comme ici. Donc chiffrons tout ça...
"je me situe comment par rapport à la tendance centrale"
ou
"je suis arrivé combientième" ?
Tendances : moyenne et écarts-types
Une fois qu'on a fait passer notre test à un vaste échantillon représentatif de la population, on va calculer la moyenne de toutes ces notes.
Cette moyenne ne nous donne pas d'indication sur la dispersion, l'étendue de la gamme de résultats. On calcule donc un second indice génial, l'écart-type (ET) : c'est en fait l'écart moyen. C'est-à-dire qu'on prend l'écart de chaque note avec la note moyenne, et on calcule la moyenne de ces écarts.
« Edit : en réalité c’est faux ! L’écart-type donne bien une indication sur la dispersion de la population en fonction des différents écarts à la moyenne. Mais il est en fait la racine carré de la variance, qui elle-même est la moyenne du carré des écarts à la moyenne : voir plus bas les explications de Sphax. »
Or, quelque soit la tête de notre courbe de Gauss, l'écart-type balise toujours les mêmes parts de population. C'est ce qui apparaît sur le graphique : entre la moyenne et moyenne + 1ET, on trouve 34,13% des individus, entre +1ET et +2ET, plus que 13,59%, etc. C'est valable quel que soit le phénomène observé, pourvu qu'on obtienne une courbe en cloche ! On apprend donc assez vite à "situer" un score exprimé en termes d'écart-type.
Pour les échelles de Weschler, pour que ce soit plus simple, on a converti ces indices en scores normalisés arbitraires : la moyenne sera 100 et l'écart-type 15, donc 115 correspond à la moyenne +1ET, etc. Ce qu'on appelle le Quotient intellectuel renvoie donc à l'écart-type, il permet de savoir à combien d'écarts-types de la moyenne on se situe.
Au-dessus de 130 comme au-dessous de 70, on ne trouve plus que 2,27% de la population. C'est ce seuil de 2ET qui a été choisi comme limite de la norme. Quant au seuil de +3ET, il représente le palier HQI/THQI : seuls 0,13% de la population ont obtenu une note supérieure à 100+(3x15), soit 145.
Lorsqu'on obtient un score exprimé en écarts-types, par exemple +2,56 ET, ou tout simplement un score de QI, la difficulté est de savoir quel pourcentage de la population se trouve au-dessus et au-dessous. Vu que notre répartition n'est pas linéaire, on est obligé de passer par une table de conversion ou des calculs un peu compliqués (ben oui, qui dit aire sous la courbe... dit intégrales !!), puisque, comme on l'a vu, il y a beaucoup plus de monde entre +1ET et +2ET qu'entre +2ET et +3ET.
Rangs : les quantièmes
Une autre solution est de s'intéresser directement à "quelle part de la population a fait mieux, quelle part a fait moins bien". Au diable la courbe de Gauss et les calculs qu'elle engendre, d'ailleurs la solution des quantièmes fonctionne même si les résultats ne suivent pas une telle courbe, contrairement aux écarts-types.
Dans ce cas, on range tous les résultats du plus petit au plus grand. On peut commencer par déterminer la médiane : la moitié de la population a fait mieux que ce score, la moitié moins bien. On peut aussi couper en 4 ou 10 pour obtenir des quartiles ou des déciles.
Mais puisque il est assez habituel de parler en pourcentages, coupons en 100 pour créer des centiles, ou percentiles ! Si alors ma note correspond au rang percentile 80, je sais que 20% ont fait mieux que moi, 80% moins bien ou équivalent. On peut même affiner les centiles, puisqu'on dit par exemple qu'une personne obtenant un QI de 144 se situe au rang percentile 99,835 (autrement dit que 99,835% de la population a obtenu un score inférieur ou équivalent).
Il semblerait que de plus en plus de psys adoptent les système des percentiles, pour éviter l'effet trompeur des scores de QI (qui cachent une réalité pas du tout linéaire). On a toutefois gardé les bornes de -2ET et +2ET pour définir la norme, bornes qui n'ont pas d'équivalents "ronds" dans le système de centiles.